Zagadka Fermata, znana również jako Wielkie Twierdzenie Fermata, to jedno z najbardziej fascynujących i trudnych wyzwań w historii matematyki. Sformułowane przez francuskiego matematyka Piotra de Fermata w XVII wieku, twierdzenie to stwierdza, że dla liczb naturalnych $$n > 2$$ nie istnieją takie liczby naturalne dodatnie $$x$$, $$y$$ i $$z$$, które spełniają równanie $$x^n + y^n = z^n$$. Pomimo że Fermat twierdził, iż posiada „zadziwiający dowód”, nie pozostawił go w swoich notatkach, co przez stulecia frustrowało i inspirowało matematyków na całym świecie.
Przez ponad 350 lat wielu wybitnych matematyków próbowało udowodnić to twierdzenie, jednak bezskutecznie. Dopiero w 1994 roku angielski matematyk Andrew Wiles zdołał przełamać ten impas, wykorzystując nowoczesne metody z teorii krzywych eliptycznych i hipotezy Shimury-Taniyamy. Jego dowód, mający około 100 stron, otworzył nową erę w teorii liczb i przyniósł mu liczne nagrody oraz uznanie w świecie matematyki.
Kluczowe informacje:
- Twierdzenie Fermata mówi, że dla $$n > 2$$ nie istnieją liczby naturalne $$x$$, $$y$$ i $$z$$, które spełniają $$x^n + y^n = z^n$$.
- Fermat zapisał swoje twierdzenie w marginesie książki, twierdząc, że ma dowód, którego nie mógł zmieścić.
- Przez 350 lat wielu matematyków próbowało udowodnić to twierdzenie, osiągając sukcesy w szczególnych przypadkach.
- Andrew Wiles udowodnił twierdzenie w 1994 roku, korzystając z teorii krzywych eliptycznych.
- Jego dowód został opublikowany w 1995 roku i przyniósł mu prestiżowe nagrody, w tym Nagrodę Abela.
Zrozumienie Twierdzenia Fermata i jego znaczenie w matematyce
Zagadka Fermata, znana również jako Wielkie Twierdzenie Fermata, to jedno z najbardziej znanych i fascynujących twierdzeń w historii matematyki. Zostało ono sformułowane przez francuskiego matematyka Piotra de Fermata w pierwszej połowie XVII wieku. Twierdzenie brzmi: dla liczby naturalnej $$n > 2$$ nie istnieją takie liczby naturalne dodatnie $$x$$, $$y$$ oraz $$z$$, które spełniają równanie $$x^n + y^n = z^n$$. To stwierdzenie, zapisane na marginesie łacińskiego tłumaczenia książki Arithmetica Diofantosa, stało się punktem wyjścia dla wielu badań i poszukiwań w matematyce.
Znaczenie zagadki Fermata wykracza daleko poza jej prostą formułę. Przez ponad 350 lat, matematycy bezskutecznie starali się udowodnić to twierdzenie, co sprawiło, że stało się ono jednym z największych wyzwań w matematyce. Pomimo licznych prób i dowodów dla szczególnych przypadków, takich jak $$n = 3$$ przez Eulera czy $$n = 5$$ przez Dirichleta, ogólny dowód pozostawał nieosiągalny. Dopiero w 1994 roku Andrew Wiles, wykorzystując nowoczesne metody, zdołał udowodnić to twierdzenie, co miało ogromne znaczenie dla rozwoju teorii liczb.
Wyjaśnienie twierdzenia Fermata oraz jego implikacje
Twierdzenie Fermata ma ogromne implikacje w matematyce, zwłaszcza w teorii liczb. Stwierdzając, że nie istnieją całkowite rozwiązania dla równania $$x^n + y^n = z^n$$ przy $$n > 2$$, otworzyło nowe kierunki badań i teorii. Jego dowód przyczynił się do rozwoju nowych narzędzi matematycznych, w tym teorii krzywych eliptycznych i form modularnych, które są kluczowe w współczesnej matematyce. Znaczenie zagadki Fermata nie ogranicza się tylko do samego twierdzenia, ale ma również wpływ na rozwój innych dziedzin matematyki, inspirując pokolenia matematyków do dalszych badań.
Historyczne konteksty i nieudane próby dowodu
Historia zagadka Fermata jest pełna znakomitych prób udowodnienia tego twierdzenia przez wielu wybitnych matematyków. Już w XVIII wieku, Leonhard Euler odniósł sukces w udowodnieniu prawdziwości twierdzenia dla przypadku $$n = 3$$. Jego dowód, choć nie był ogólny, przyczynił się do dalszego zrozumienia problemu. Kolejnym ważnym krokiem był dowód dla $$n = 5$$, który został przedstawiony przez Joseph-Louis Lagrange'a. Lagrange, podobnie jak Euler, nie dostarczył jednak ogólnego rozwiązania, co pozostawiło wiele pytań otwartych.
W XIX wieku, Ernst Eduard Kummer podjął się wyzwania udowodnienia twierdzenia dla nieskończonej liczby wykładników, co również nie przyniosło oczekiwanego rezultatu. Jego prace wprowadziły nowe koncepcje, takie jak pojęcie idealnych liczb, które miały na celu zrozumienie problemu. Pomimo tych wysiłków, Wielkie Twierdzenie Fermata pozostawało nieudowodnione przez ponad 350 lat, co czyniło je jednym z największych wyzwań w historii matematyki. Dopiero w latach 90. XX wieku, dzięki pracy Andrew Wilesa, zagadka ta znalazła swoje rozwiązanie.
Kluczowe etapy dowodu Wilesa i ich znaczenie
Dowód zagadka Fermata autorstwa Andrew Wilesa składa się z kilku kluczowych etapów, które miały ogromne znaczenie dla matematyki. Pierwszym krokiem było zrozumienie związku między krzywymi eliptycznymi a formami modularnymi. Wiles skoncentrował się na hipotezie Shimury-Taniyamy, która sugerowała, że każda krzywa eliptyczna jest związana z odpowiednią formą modularną. Następnie, Wiles zastosował techniki z teorii liczb, aby skonstruować dowód, który mógłby połączyć te dwa obszary matematyki. Kluczowym momentem było udowodnienie, że pewne właściwości form modularnych mogą być użyte do analizy rozwiązań równania Fermata.
| Krok | Opis |
|---|---|
| 1. Zrozumienie hipotezy Shimury-Taniyamy | Wiles skupił się na powiązaniu między krzywymi eliptycznymi a formami modularnymi. |
| 2. Zastosowanie teorii liczb | Wykorzystanie technik z teorii liczb do analizy rozwiązań równania Fermata. |
| 3. Połączenie krzywych eliptycznych i form modularnych | Dowód, że właściwości form modularnych mogą być użyte w kontekście zagadki Fermata. |
Wpływ dowodu Wilesa na współczesną matematykę
Dowód Wilesa na wielkie twierdzenie Fermata miał znaczący wpływ na współczesną matematykę, otwierając nowe kierunki badań. Jego prace przyczyniły się do rozwoju teorii krzywych eliptycznych oraz form modularnych, które stały się kluczowymi elementami w wielu obszarach matematyki. Po publikacji dowodu, wiele badań skoncentrowało się na zastosowaniu tych teorii w innych problemach matematycznych, co przyczyniło się do postępu w dziedzinach takich jak teoria liczb i geometria algebraiczna. Wiles stał się inspiracją dla wielu matematyków, którzy podjęli się badań w obszarach związanych z jego odkryciami.
Matematyczne koncepcje związane z twierdzeniem Fermata
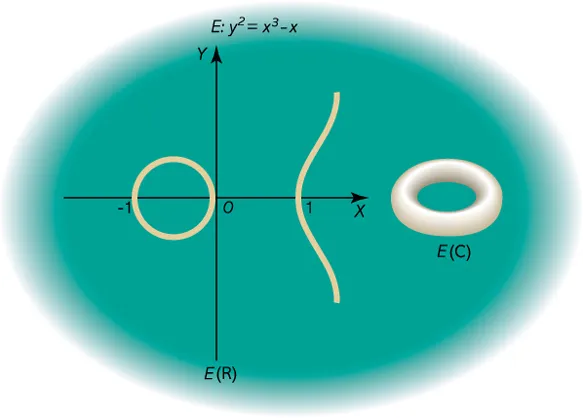
Krzywe eliptyczne to istotny element w badaniach nad zagadka Fermata. Są to krzywe opisane równaniami w postaci $$y^2 = x^3 + ax + b$$, gdzie a i b są stałymi. Krzywe eliptyczne mają wiele zastosowań w teorii liczb, kryptografii oraz geometrii algebraicznej. W kontekście twierdzenia Fermata, krzywe eliptyczne odgrywają kluczową rolę w połączeniu z formami modularnymi, co umożliwiło Wilesowi opracowanie dowodu. Ich struktura i właściwości matematyczne pozwalają na głębsze zrozumienie problemów związanych z liczbami całkowitymi oraz ich rozwiązaniami.
Formy modularne są kolejnym ważnym aspektem w badaniach nad wielkim twierdzeniem Fermata. Są to funkcje holomorficzne, które spełniają określone warunki symetrii. Formy modularne są ściśle związane z krzywymi eliptycznymi, co stanowi fundament hipotezy Shimury-Taniyamy. Dzięki tej hipotezie, matematycy mogą badać właściwości krzywych eliptycznych poprzez formy modularne. W kontekście dowodu Wilesa, zrozumienie tych dwóch koncepcji było kluczowe dla połączenia różnych dziedzin matematyki i rozwiązania zagadki, która pozostawała nierozwiązana przez wieki.
Zastosowanie krzywych eliptycznych w dowodzie Wilesa
W dowodzie Wilesa na zagadka Fermata, krzywe eliptyczne były wykorzystywane do zbudowania połączenia z formami modularnymi. Wiles zademonstrował, że krzywe eliptyczne związane z rozwiązaniami równania Fermata mogą być klasyfikowane jako formy modularne. To odkrycie miało kluczowe znaczenie, ponieważ pozwoliło na zastosowanie wyników z teorii form modularnych do analizy krzywych eliptycznych. Dzięki temu, Wiles był w stanie wykazać, że twierdzenie Fermata jest prawdziwe, łącząc te dwa obszary matematyki w nowatorski sposób. Krzywe eliptyczne stały się więc narzędziem, które umożliwiło rozwiązanie problemu, który przez wieki wydawał się nieosiągalny.
Rola form modularnych w teorii liczb
Formy modularne są kluczowym elementem w teorii liczb, a ich znaczenie stało się szczególnie widoczne w kontekście wielkiego twierdzenia Fermata. Te funkcje holomorficzne, które spełniają określone warunki symetrii, mają zastosowanie w różnych dziedzinach matematyki, w tym w kryptografii oraz analizie matematycznej. W kontekście zagadki Fermata, formy modularne stanowią most łączący różne obszary matematyki, umożliwiając badanie właściwości krzywych eliptycznych. Dzięki hipotezie Shimury-Taniyamy, matematycy zyskali nowe narzędzia do analizy i zrozumienia relacji między tymi dwiema dziedzinami. To połączenie było kluczowe dla rozwoju nowoczesnej matematyki i przyczyniło się do wielu postępów w teorii liczb.
Dziedzictwo twierdzenia Fermata w matematyce i kulturze
Dziedzictwo zagadka Fermata jest ogromne, zarówno w matematyce, jak i w kulturze. Po rozwiązaniu tego problemu przez Andrew Wilesa, matematyka zyskała nowe kierunki badań, a jego dowód otworzył drzwi do dalszych odkryć w teorii liczb. Wpływ tego twierdzenia widać w licznych badaniach, które badają krzywe eliptyczne i formy modularne. Współczesna matematyka, w dużej mierze, korzysta z narzędzi i koncepcji, które wyewoluowały w wyniku poszukiwań związanych z twierdzeniem Fermata, co podkreśla jego znaczenie w historii nauki.
Oprócz wpływu na matematykę, wielkie twierdzenie Fermata znalazło swoje miejsce w popkulturze. Wiele książek, filmów i programów telewizyjnych odnosi się do tej zagadki, podkreślając jej tajemniczość i trudności związane z jej rozwiązaniem. Przykładem może być powieść "The Man Who Knew Infinity", która opowiada o życiu matematyka Srinivasa Ramanujana, a także o jego relacji z matematycznym światem. Takie przedstawienia przyciągają uwagę społeczeństwa do matematyki, czyniąc ją bardziej przystępną i interesującą dla szerszej publiczności.
Praktyczne zastosowania teorii liczb w nowoczesnej technologii
Teoria liczb, w tym koncepcje związane z krzywymi eliptycznymi i formami modularnymi, ma ogromny potencjał w dziedzinie nowoczesnej technologii, zwłaszcza w zakresie kryptografii. Współczesne systemy zabezpieczeń, takie jak protokoły szyfrowania, często opierają się na trudnych problemach matematycznych, które mają swoje korzenie w teorii liczb. Użycie krzywych eliptycznych w algorytmach szyfrowania, takich jak ECDSA (Elliptic Curve Digital Signature Algorithm), pozwala na stworzenie bardziej bezpiecznych i efektywnych systemów, które są mniej podatne na ataki.
W przyszłości możemy spodziewać się dalszego rozwoju technologii opartych na matematyce, co może prowadzić do jeszcze bardziej zaawansowanych metod zabezpieczeń. Znaczenie zagadki Fermata i jej rozwiązania przez Andrew Wilesa może inspirować nowe pokolenia matematyków i inżynierów do poszukiwania innowacyjnych rozwiązań w dziedzinie informatyki i technologii. Przykłady zastosowań obejmują rozwój algorytmów dla systemów blockchain, które również korzystają z zaawansowanych koncepcji matematycznych, co pokazuje, jak teoria liczb wpływa na nasze codzienne życie i nowoczesne technologie.
